Question

(PLEASE HELP ASAP)

Consider the system of equations shown below:


`3x_(1)+ x_(2)-x_(3)=4\\x_(2)+5x_(3)=-1\\4x_(1)+5x_(2)+5x_(3)=8`


A. If the system of equations is represented by a matrix equation Ax = b, where x =
`\left[\begin{array}{ccc}x_(1) \\x_(2) \\x_(3) \end{array}\right]` and b =
`\left[\begin{array}{ccc}4\\-1\\8\end{array}\right]`, then what is the size f matrix A? Explain you reasoning.


B. What are the entries, in order from left to right, in the second row of A? Explain your reasoning.


C. Suppose that more equations, but not more variables, were included in the system of equations above. How would the size of matrix A and the sizes of vectors x and b change, if at all? Explain and be specific about any changes you describe.

Answer 1

9514 1404 393

Answer:

A. 3×3

B. [0, 1, 5]

C. (rows, columns) = (# equations, # variables) for matrix A; vector x remains unchanged; vector b has a row for each equation.

Explanation:

A. The matrix A has a row for each equation and a column for each variable. The entries in each column of a given row are the coefficients of the corresponding variable in the equation the row represents. If the variable is missing, its coefficient is zero.

This system of equations has 3 equations in 3 variables, so matrix A has dimensions ...

A dimensions = (rows, columns) = (# equations, # variables) = (3, 3)

Matrix A is 3×3.

__

B. The second row of A represents the second equation:

`0x_1+1x_2+5x_3=-1`

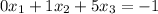
The coefficients of the variables are 0, 1, 5. These are the entries in row 2 of matrix A.

__

C. As stated in part A, the size of matrix A will match the number of equations and variables in the system. If the number of variables remains the same, the number of rows of A (and b) will reflect the number of equations. (The number of columns of A (and rows of x) will reflect the number of variables.)