Question

The product of two numbers is 4, while their sum is 52. Find the sum of the reciprocals of the numbers. Work shown pls!

Answer 1

`13`

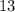
Explanation:

Given :-

• The sum of two numbers is 52.
• The product of the numbers is 4 .

And we need to find the sum of reciprocals of the numbers. For that let us assume that the numbers are
`x \ \& \ y` .

According to 1st condition :-

`\implies x + y = 52`

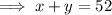
Now expressing this equation by keeping only one variable on one side as ,

`\implies x = 52 - y`

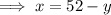
According to 2nd condition :-

`\implies x y = 4 \\\\\implies (52-y)y = 4 \\\\\implies 52 y - y^2 = 4 \\\\\implies y^2 - 52y + 4 = 0`

• Now solve this quadratic equation.

On solving the equation using quadratic Formula we will get the value of y as ,

`\implies y = 26\pm 4√(42)`

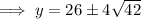
• Note that the sum of x and y is 52 .So in order to find the value of x we will subtract 26±4√42 from 52 and we will get the value of x same as y .

`\implies x = 52 - 26\pm 4√(42) = 26\pm 4√(42)`

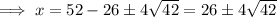
Now we need to find out the sum of reciprocal of the two numbers . That will be ,

`\implies (1)/(26+4√(42))+ (1)/(26-4√(42)) \\\\\implies (26+4√(42)+26-4√(42))/((26+4√(42))(26-4√(42))\\\\\implies (52)/((26)^2-(4√(42))^2) \\\\\implies (52)/(676-672) \\\\\implies (52)/( 4) \\\\\implies \boxed{\red{13}}`

Hence the sum of their reciprocals is 13 .