Answer:
The area of this triangle is about 21.2132 square units.
Explanation:
First, find the lengths of the legs AB and BC.
Length of AB ===
Find the difference in position vertically:

The points are 6 units apart vertically.
Find the difference in position horizontally:
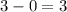
The points are 3 units apart horizontally.
These lengths form a right triangle with the distance between the points as the hypotenuse, so you can use the pythagorean theorem to solve:

AB is about 6.7082 units long.
Length of BC ===
Same process as above.
Find the vertical distance:
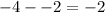
2 units apart vertically.
Find the horizontal distance:
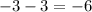
6 units apart horizontally.
Use the pythagorean theorem:
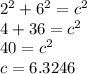
BC is about 6.3246 units long.
Area ===
Finally, you can use these to find the area of the triangle. The area of a right triangle is just half the area of a rectangle with the same base and height:
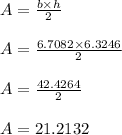
The area of this triangle is about 21.2132 square units.