Answer:
7.1
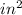
Explanation:
The surface of an ice-hockey puck is shaped as a circle. This means that the surface area of this circle is calculated by the following formula
A=
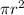
If the measurement of one side to the other is 3 inches, this would be the diameter. The radius is half of the diameter, so in this scenario, it would be 1.5 inches. We can now plug this value into the formula and solve for the surface area.
A =
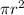
A =
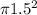
A =
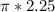
A = 7.068 or 7.1
 (rounded to the nearest tenth)
(rounded to the nearest tenth)