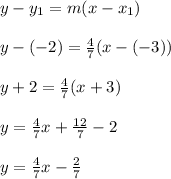Answer:
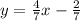
Step-by-step explanation:
The equation of a straight line is given by:
y = mx + b;
where y, x are variables, m is the slope of the line and b is the y intercept.
If two lines are parallel to each other, then they have the same slope, i.e. their slopes are equal.
The equation of a line passing through the point (-3, -2) and parallel to the line y = (4/7)x - 3, would have the same slope as the line y = (4/7)x - 3
The slope (m) of the line y = (4/7)x - 3 is 4/7, hence the line passes through the point (-3, -2) with a slope of 4/7.
The equation of the line is given by: