Question

XY is a diameter of a circle and Z is a point on the circle such that ZY=6. If the area of the triangle XYZ is 18 square root 3 find the length of arc XZ

Answer 1

4π

Explanation:

As shown in the diagram, triangle XYZ is a right triangle. Therefore, its area (A) is given by:

A =
`(1)/(2)` x b x h -------------(i)

Where;

A = 18
`√(3)`

b = XZ = base of the triangle

h = YZ = height of the triangle = 6

Substitute these values into equation(i) and solve as follows:

18
`√(3)` =
`(1)/(2)` x b x 6

18
`√(3)` = 3b

Divide through by 3

6
`√(3)` = b

Therefore, b = XZ = 6
`√(3)`

Now, assume that the circle is centered at O;

Triangle XOZ is isosceles, therefore the following are true;

(i) |OZ| = |OX|

(ii) XZO = ZXO = 30°

(iii) XOZ + XZO + ZXO = 180° [sum of angles in a triangle]

=> XOZ + 30° + 30° = 180°

=> XOZ + 60° = 180°

=> XOZ = 180° - 60°

=> XOZ = 120°

Therefore we can calculate the radius |OZ| of the circle using sine rule as follows;

`(sin|XOZ|)/(XZ) = (sin|ZXO|)/(OZ)`

`(sin120)/(6√(3) ) = (sin 30)/(OZ)`

`(√(3) /2)/(6√(3) ) = (1/2)/(|OZ|)`

`(1)/(12) = (1)/(2|OZ|)`

`(1)/(6) = (1)/(|OZ|)`

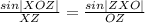
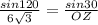
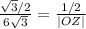
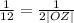
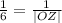
|OZ| = 6

The radius of the circle is therefore 6.

Now, let's calculate the length of the arc XZ

The length(L) of an arc is given by;

L = θ / 360 x 2 π r ------------------(ii)

Where;

θ = angle subtended by the arc at the center.

r = radius of the circle.

In our case,

θ = ZOX = 120°

r = |OZ| = 6

Substitute these values into equation (ii) as follows;

L = 120/360 x 2π x 6

L = 4π

Therefore the length of the arc XZ is 4π