Answer:
They would have to do 407 such checks.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the z-score that has a p-value of
 .
.
The margin of error is of:

Kroll, Inc., a firm that specializes in investigating such matters, said that they believe as many as 25% of back ground checks might reveal false information.
This means that
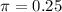
98% confidence level
So
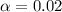 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
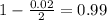 , so
, so
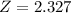 .
.
How many such random checks would they have to do to esti mate the true percentage of people who misrepresent their backgrounds to within ±5% with 98% confidence?
This is n for which M = 0.05. So

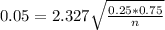
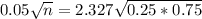


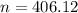
Rounding up:
They would have to do 407 such checks.