Answer:
Range: 19
Interquartile range: 6.5
Variance: 44.86
Standard deviation: 6.70
Explanation:
Given set:
27, 25, 20, 15, 30, 34, 28, 25.
(i) Range is the difference between the largest value and smallest value in a given data.
In the data above, the;
largest value = 34
smallest value = 15
Range = largest - smallest
Range = 34 - 15
Range = 19
(ii) Interquartile range is the difference between the median (Q₁) of the lower half of the given data, and the median (Q₃) of the upper half of the given data. i.e Q₃ - Q₁.
This should be done after ordering the given data in ascending order.
Ordering the above data gives:
15, 20, 25, 25, 27, 28, 30, 34
In the data above;
lower half = 15, 20, 25, 25
upper half = 27, 28, 30, 34
Find median (Q₁) of the lower half
Since there are even number of data, the median is the average of two middle numbers (20 and 25) i.e.
Q₁ =
=
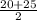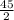= 22.5
Find median (Q₃) of the upper half
Since there are even number of data, the median is the average of two middle numbers (28 and 30) i.e.
Q₃ =
=
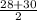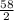= 29
Interquartile range = Q₃ - Q₁
Interquartile range = 29 - 22.5
Interquartile range = 6.5
(iii) Variance is the measure of variability of a given set of data. It is calculated by following these steps:
=> First find the mean of the data by summing the numbers and dividing by the number of numbers. i.e
mean(x) = [15 + 20 + 25 + 25 + 27 + 28 + 30 + 34] / 8
mean(x) = [204] / 8
mean(x) = 25.5
=> Next, get the mean deviation by subtracting the mean from each individual value in the given set of data. i.e
15 - 22.5 = -7.5
20 - 22.5 = -2.5
25 - 22.5 = 2.5
25 - 22.5 = 2.5
27 - 22.5 = 4.5
28 - 22.5 = 5.5
30 - 22.5 = 7.5
34 - 22.5 = 11.5
=> Next, find the square of each of the results obtained above. i.e
(-7.5)² = 56.25
(-2.5)² = 6.25
(2.5)² = 6.25
(2.5)² = 6.25
(4.5)² = 20.25
(5.5)² = 30.25
(7.5)² = 56.25
(11.5)² = 132.25
=> Next, add all the results above together as follows;
56.25 + 6.25 + 6.25 + 6.25 + 20.25 + 30.25 + 56.25 + 132.25 = 314
=> Now, obtain the variance by dividing the result above one less than the number of numbers.
The number of numbers is 8. One less than this gives 7.
Therefore,
Variance = 314 / 7
Variance = 44.86
(iv) Standard deviation is the measure of how the numbers in the given data are spread out. It is calculated as the square root of variance.
Therefore,
Standard deviation = √variance.
Variance has been calculated above.
Standard deviation = √44.86
Standard deviation = 6.70