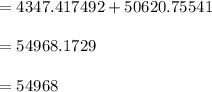Question

Paulina Lesky is 27 years old and has accumulated $7,500 in her self-directed defined contribution pension plan. Each year she contributes $2,000 to the plan, and her employer contributes an equal amount. Paulina thinks she will retire at age 63 and figures she will live to age 90. The plan allows for two types of investments. One offers a 3% risk-free real rate of return. The other offers an expected return of 12% and has a standard deviation of 39%. Paulina Lesky is 27 years old and has accumulated $7,500 in her self now has 20% of her money in the risk-free investment and 80% in the risky investment. She plans to continue saving at the same rate and keep the same proportions invested in each of the investments. Her salary will grow at the same rate as inflation. How much can Paulina be sure of having in the safe account at retirement?

A) $45,473.
B) $62,557.
C) $78,943.
D) $54,968.
E) $74,643.

Answer 1

The answer is "Option D".

Step-by-step explanation:

The amount accrued in the pension system until now
`= 7500`

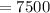
Danger or security account proportion
`= 20 \%`

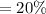
The percentage of the amount kept in a safe account
`(PV) = 7500* 20\% = 1500\%`

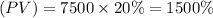
Number of investment years owned by
`(n)=63-27=36`

Risk-free return rate
`I = 3\%`

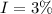
Combined total amount up to age 63 (formula for the current value) =
`Present \ value* (1+i)^n`

`=1500* (1+3\%)^(36)\\\\=4347.417492`

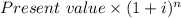
The contribution is
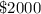`\$2000` a year and the employer corresponds with the same amount for the pension plan.

Total annual contribution
`= 2000+2000 = 4000`

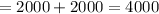
Risk-free or healthy account proportion
`= 20\%`

Amount invested annually
`(P) = 4000* 20\% = 800 \ (Risk \ free)`

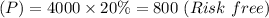
Annual deposit amount (n) for years
`=63-27 =36`

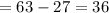
Returns free of risk
`I = 3\%`

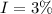
An cumulative sum due to an annuity
`= P* ((((1+i)^n)-1))/(i)`

`=800* ((((1+3\%)^(36))-1))/(3\%)\\\\=50620.75541`

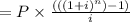
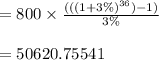
Total amount accumulated in safe account
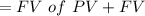`= FV\ of \ PV + FV` of annuity

`=4347.417492+50620.75541\\\\=54968.1729\\\\=54968`