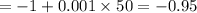Answer:
The answer is "Option b".
Explanation:
In the given question, 1000 ticket were sold for
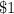 and the owner who receives tickets which are randomly chosen that wins
and the owner who receives tickets which are randomly chosen that wins
 .
.
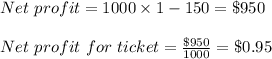
The probability in which each ticket owners win
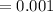
therefore the ticket owner net profit =