Question

In a class, we have 61 students of different majors. There are 23 chemistry majors (C), 12 math majors (M), 9 engineering majors (E), and 17 students who are undecided (U). Of these students, 4 of them have declared both math and engineering majors. A student will randomly be chosen to win a scholarship.

Suppose that we decide to award three scholarships. What is the probability that the first winner is a chemistry major, the second winner is a chemistry major, and the third winner is an undecided major? (A student cannot win more than one scholarship).
a. 0.3096.
b. 1.0319.
c. 0.0398.
d. 0.9604.

Answer 1

c. 0.0398.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

To solve this question, we find each separate probability, and then multiply them.

First winner is a chemistry major

23 chemistry majors out of 61 students. So

`P(A) = (23)/(61)`

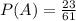
Second winner is a chemistry major:

Considering the first event, 22 chemistry majors out of 60 students. So

`P(B) = (22)/(60)`

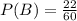
Third winner is an undecided major;

Considering the first two events, 17 undecided out of 59 students. So

`P(C) = (17)/(59)`

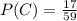
Desired probability:

`P(A \cap B \cap B) = P(A)P(B)P(C) = (23)/(61) * (22)/(60) * (17)/(59) = (23*22*17)/(61*60*59) = 0.0398`

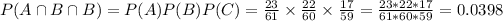
So option c.