Question

A solid circular rod that is 600 mm long and 20 mm in diameter is subjected to an axial force of P = 50 kN. The elongation of the rod is delta = 1.40 mm and its diameter becomes df = 19.9837 mm. Determine the modulus of elasticity (E) and the modulus of elasticity in shear (G). Assume the material does not yield.

Answer 1

a) the modulus of elasticity (E) is 68.22 GPa

b) the modulus of elasticity in shear is 25.28 GPa

Step-by-step explanation:

Given the data in the question;

First we determine the cross-sectional area A of the road;

A = π/4 × d²

given that; diameter d = 20 mm

we substitute

A = π/4 × ( 20 mm )²

A = π/4 × 400 mm

A = 314.159 mm²

Next, we find, the normal stress of the rod σ

σ = P / A

given that load p = 50 kN = 50,000 Newton

we substitute

σ = 50,000 N / 314.159 mm²

σ = 159.155 N/mm²

σ = 159.155 Mpa

Next, is the normal strain ε

ε = δ / L

given that; change in length δ = 1.40 mm and Length of rod L = 600 mm

we substitute

ε = 1.40 mm / 600 mm

ε = 0.002333

Now, we find the modulus of elasticity;

we know that;

σ = Eε

modulus of elasticity E = σ / ε

we substitute

E = 159.155 Mpa / 0.002333

E = 68219.031 MPa

E = ( 68219.031 / 1000 ) GPa

E = 68.22 GPa

Therefore, the modulus of elasticity (E) is 68.22 GPa

b)

we know that the Poisson's ratio v is;

v = -(ε
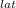`_{lat` / ε )

v = - (((d
`_f` - d)/d) / ε )

where d
`_f` is the final diameter of the rod ( 19.9837 mm ) and ε
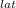`_{lat` is the lateral strain

so we substitute

v = - ((( 19.9837 - 20 ) / 20 ) / 0.002333 )

v = - (( -0.0163 / 20 ) / 0.002333 )

v = - ( - 0.000815 / 0.002333 )

v = - ( - 0.3493 )

v = 0.3493

So, our shear modulus will be;

G = E / 2( 1 + v )

we substitute

G = 68.22 GPa / 2( 1 + 0.3493 )

G = 68.22 GPa / 2( 1.3493 )

G = 68.22 GPa / 2.6986

G = 25.28 GPa

Therefore, the modulus of elasticity in shear is 25.28 GPa