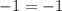Answer:
(a) Neither
(a) Perpemdicular
Explanation:
Required
Determine the relationship between given lines
(a)
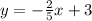
and
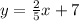
An equation written in form:
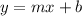 has the slope:
has the slope:
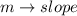
So, in both equations:
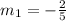
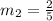
For both lines to be parallel
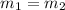
This is false in this case, because:
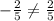
For both lines to be perpendicular
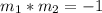
This is false in this case, because:

(b)

and
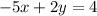
Write equations in form:
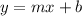

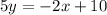
Divide by 5
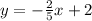
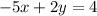

Divide by 2
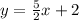
In both equations:
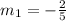

For both lines to be parallel
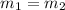
This is false in this case, because:
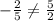
For both lines to be perpendicular
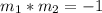
This is true in this case, because:
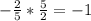
Cancel out 2 and 5