Question

A group of students wants to determine the internal resistance of a battery. They connect the battery to a variable resistor. The students measure the potenial differnce across the battery as a function of the current throught the battery as they vary the resistance. Which of the following analyses of the data could be used to determine the internal resistance of the battery?

A. Divide the potential difference across the battery by the current through it for each data point. The average of these calculations gives the internal resistance of the battery.
B. Graph the potential difference across the battery as a function of the current through it. Extrapolate to find the y- intercept and divide this by the average of the current measurements to find the internal resistance of the battery.
C. Find the best-fit straight line for a graph of potential difference across the battery as a function of the current through it. The absolute value of the slope represents the internal resistance of the battery.
D. This data cannot be analyzed to give the internal resistance of the battery, because the potential difference across the battery does not depend on the current.

Answer 1

The answer is "Option C"

Step-by-step explanation:

Ohm's Rule we remember
`V = I* R`

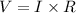
It looks like the sample is drawn y=mx while m is curve slope

The slope of the graph is its resistance if they draw a graph v vs I.

However, the internal battery presence resistance can be modified as the straight line equation

`y = mx -c`

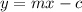
where c is y-intercept:

`E = I(R+r) \\\\ E = IR+ Ir\\\\E = V + Ir\\\\V = E- Ir\\\\V = -Ir+E`

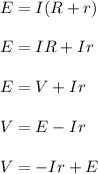
R is really the internal battery resistance to draw graph V vs I, the slope is internal resistance to the negative slope cure.