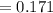Question

The Regency Hotel has enough space at its entrance for six taxicabs to line up, wait for guests, and then load passengers. Cabs arrive at the hotel every 8 minutes; if a taxi drives by the hotel and the line is full, it must drive on. Hotel guests require a taxi every 5 minutes, on average. It takes a cab driver an average of 3.5 minutes to load passengers and luggage and leave the hotel(exponentially distributed).

1. What is the average time a cab must wait for a fare?
2. What is the probability that the line will be full when a cab drives by, causing it to drive on?

Answer 1

The appropriate solution is:

(1) 22.81 minutes

(2) 0.171

Explanation:

According to the question, the values will be:

The service rate of guess will be:

=
`5+3.5`

=
`8.5 \ minutes`

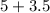
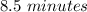
The mean arrival rate will be:

`\lambda =(60)/(5)`

`=7.5 \ cabs/hr`

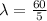
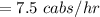
The mean service rate will be:

`\mu= 7.05 \ cabs/hr`

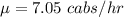
(1)

The average time a cab must wait will be:

⇒
`W_q=22.95-(1)/(7.05)`

⇒
`=(161.798-1)/(7.05)`

⇒
`=(160.798)/(7.05)`

⇒
`=22.81 \ minutes`

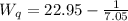
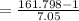
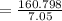
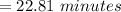
(2)

The required probability will be:

⇒
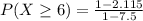
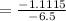
`P(X\geq 6)=(1-2.115)/(1-7.5)`

⇒
`=(-1.1115)/(-6.5)`

⇒
`=0.171`