Question

Suppose a poll is taken that shows that 281 out of 500 randomly selected, independent people believe the rich should pay more taxes than they do. Test the hypothesis that a majority (more than 50%) believe the rich should pay more taxes than they do. Use a significance level of 0.05.

Answer 1

The claim is true.

Explanation:

Given - Suppose a poll is taken that shows that 281 out of 500 randomly selected, independent people believe the rich should pay more taxes than they do.

To find - Test the hypothesis that a majority (more than 50%) believe the rich should pay more taxes than they do. Use a significance level of 0.05.

Solution -

Given that,

X = 281, n = 500

So,

The hypothesis are :

H0 : p = 0.50

H1 : p > 0.50

So,

Sample proportion is

p bar = X/n

= 281/500

= 0.562

⇒p bar = 0.562

Now,

Test statistics :

`Z_(0) = \frac{p bar - p}{\sqrt{(p(p - 1))/(n) } } \\= \frac{0.562 - 0.50}{\sqrt{(0.50(0.50 - 1))/(500) } }\\= 0.277`

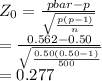
∴ we get

`Z_(0) = 0.277`

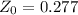
SO,

p-value = P( Z ≥ 0.277)

= 1 - P(Z ≤ 0.277)

= 1 - 0.997

= 0.002779

∴ we get

The conclusion is -

As
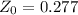`Z_(0) = 0.277` > Z = 1.645

We reject H0

And

We have enough information to conclude that the population proportion is greater than 0.50

So,

The claim is true.