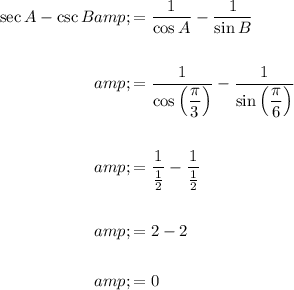Question

.

If sin (A + B) = 1 and tan (A - B) = 1/v3, find the value of:
i) tan A+ tan B
ii) sec A- cosec B
​

Answer 1

Given :-

If sin (A + B) = 1

and tan (A - B) = 1/√3

To Find :-

value of:

• i) tan A+ tan B
• ii) sec A- cosec B

Solution :-

We know that,

• sin 90 = 1
• tan 30 = 1/√3

So,

• sin(A + B) = sin90
• (A+B)=90

• tan(A - B) =tan 30
• (A-B)=30

A + B + A - B = 90 + 30

(A + A) + (B - B) = 120

2A = 120

A = 120/2

• A = 60

By putting value of A in 2

A - B = 30

60 - B = 30

-B = 30 - 60

-B = -30

• B = 30

Finding values

tan 60 + tan 30

We know that

• tan 60 = √3
• tan 30 = 1/√3

√3 + 1/√3

√3 × √3 + 1/√3

3 + 1/√3

`4/√3`

sec A- cosec B

sec 60 - cosec 30

We know that

• sec 60 = 2
• cosec 30 = 2

2 - 2 =
`0`

Hence,

tan A+ tan B=4/√3

sec A- cosec B=0

Answer 2

`\textsf{i)}\quad \tan A + \tan B=(4√(3))/(3)`

`\textsf{ii)} \quad \sec A - \csc B=0`

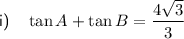
Explanation:

The given trigonometric equations are:

`\sin(A+B)=1`

`\tan(A-B)=(1)/(√(3))`

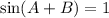
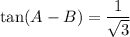
By referring to the unit circle, we know that sinθ = 1 when θ = π/2. Therefore, we can express the value 1 as sin(π/2):

`\begin{aligned}\sin(A+B)&=1\\\\\sin(A+B)&=\sin \left((\pi)/(2)\right)\\\\A+B&=(\pi)/(2)\end{aligned}`

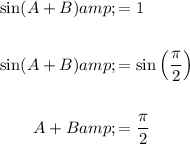
By referring to the unit circle, we find that sinθ/cosθ = 1/√3 when θ = π/6. As a result, we can represent the value 1/√3 as tan(π/6):

`\begin{aligned}\tan(A-B)&=(1)/(√(3))\\\\\tan(A-B)&=\tan \left((\pi)/(6)\right)\\\\A-B&=(\pi)/(6)\end{aligned}`

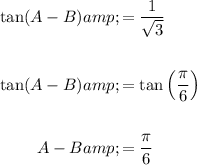
Combine the equations to eliminate B, and then solve for A:

`\begin{aligned}A+B+A-B&=(\pi)/(2)+(\pi)/(6)\\\\2A&=(2\pi)/(3)\\\\A&=(\pi)/(3)\end{aligned}`

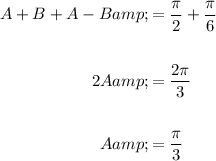
Substitute the found value of A into the equation for A + B and solve for B:

`\begin{aligned}A+B&=(\pi)/(2)\\\\(\pi)/(3)+B&=(\pi)/(2)\\\\B&=(\pi)/(2)-(\pi)/(3)\\\\B&=(\pi)/(6)\end{aligned}`

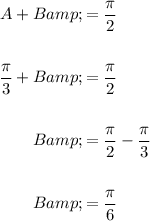
Therefore, the values of A and B are:

`A=(\pi)/(3)\qquad B=(\pi)/(6)`

Now that we have found the values of A and B, we can evaluate the given expressions.

Calculate tan A + tan B:

`\begin{aligned}\tan A + \tan B &=\tan \left((\pi)/(3)\right)+\tan \left((\pi)/(6)\right)\\\\&=√(3)+(√(3))/(3)\\\\&=(3√(3))/(3)+(√(3))/(3)\\\\&=(4√(3))/(3)\end{aligned}`

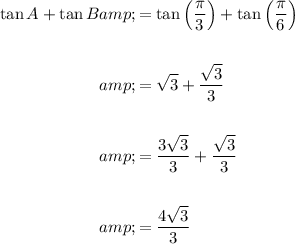
Calculate sec A + csc B:

`\begin{aligned}\sec A - \csc B&=(1)/(\cos A)-(1)/(\sin B)\\\\&=(1)/(\cos \left((\pi)/(3)\right))-(1)/(\sin\left((\pi)/(6)\right))\\\\&=(1)/((1)/(2))-(1)/((1)/(2))\\\\&=2-2\\\\&=0\end{aligned}`