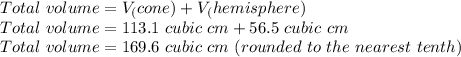Question

Find the total volume of ice cream if the ice cream completely fills the cone shown and then creates a hemisphere on top of the cone, where the cone has a diameter of 6 cm and a height of 12 cm. Round your final answer to the nearest tenth of a cubic centimeter.

Answer 1

The total volume of the ice cream, when the cone is completely filled and a hemisphere is added on top, is approximately
`169.6 \ cubic \ cm.`

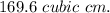
Explanation:

To find the total volume of the ice cream, we need to calculate the volume of the cone and the volume of the hemisphere separately, and then add them together.

First, let's find the volume of the cone. The formula for the volume of a cone is
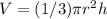`V = (1/3)\pi r^2h` , where
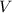`V` is the volume,
`r` is the radius, and
`h` is the height.

Given that the cone has a diameter of
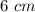`6 \ cm` , we can find the radius by dividing the diameter by 2. So, the radius
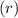`(r)` of the cone is
`6 \ cm / 2 = 3 \ cm.`

The height
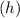`(h)` of the cone is given as
`12 \ cm.`

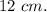
Now, we can substitute the values into the formula and calculate the volume of the cone:

`V_(cone) = (1/3) \pi (3 cm)^2(12 cm)\\V_ (cone ) = 113.1 \ cubic \ cm \ (rounded \ to \ the \ nearest \ tenth)\\`

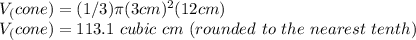
Next, let's find the volume of the hemisphere. The formula for the volume of a hemisphere is
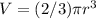`V = (2/3)\pi r^3` , where
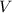`V` is the volume and
`r` is the radius.

Since the radius of the cone and the hemisphere is the same
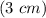`(3 \ cm)`, we can use the same value.

Now, we can substitute the value into the formula and calculate the volume of the hemisphere:

`V_ (hemisphere) = (2/3) \pi (3 cm)^3\\V_(hemisphere) = 56.5 \ cubic \ cm \ (rounded \ to \ the \ nearest \ tenth)\\`

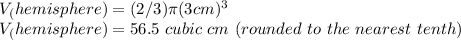
Finally, we add the volume of the cone and the volume of the hemisphere together to find the total volume of the ice cream:

`Total \ volume = V_(cone) + V_(hemisphere)\\Total \ volume = 113.1 \ cubic \ cm + 56.5 \ cubic \ cm\\Total \ volume= 169.6 \ cubic \ cm \ (rounded \ to \ the \ nearest \ tenth)\\`