Answer:
See below
Explanation:
Finding a:
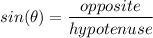
Where θ = 45° , opposite = a, hyp = 4√2
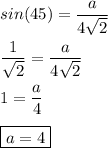
Finding c:
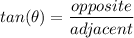
Where θ = 45°, opposite = 4, adjacent = c
tan 45 = 4 / c
1 = 4 / c
Multiply both sides by c
c = 4
Finding b:
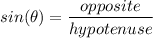
Where θ = 30°, opposite = a(4), hypotenuse = b
sin 30 = 4 / b
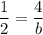
Cross Multiply
1 * b = 4 * 2
b = 8
Finding d:
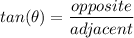
Where θ = 30°, opposite = a(4) , adjacent = d
tan 30 = 4 / d
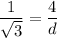
Cross Multiplying
1 * d = 4√3
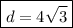
![\rule[225]{225}{2}](https://img.qammunity.org/2022/formulas/mathematics/high-school/3icqlwn6du2l5ygbr7z2lp6sjjralcpq09.png)
Hope this helped!
~AH1807