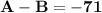Given :-
The difference between two positive numbers is 7 and the difference between these cubes is 805. If 'A' represents their product and 'B' represents the sum of their squares,
To Find :-
Solution :-
So,
Let the number be n and m
A = n × m = nm
B = n² + m² = (n + m)²
Now
n³ - m³ = 805
(n - m) (n² + m² + nm) = 805
Since difference is 7
7 × n² + m² + nm = 805
n² + m² + nm = 805/7
n² + m² + nm = 115
(n² + n) + (m² + m) = 115
A + B = 115
Now
On squaring the first eq.
(n - m)² = (7)²
(n - m)² = 49
B - 2A = 49
Now
A + B - B + 2A = 115 - 49
A + 2A = 66
3A = 66
A = 66/3
A = 22
By using 2
B - 2(22) = 49
B - 44 = 49
B = 49 + 44
B = 93
A - B = 22 - 93 = -71