Question

Help please I'm terrible at trigonometry

Two girls are standing 100 feet apart. They both see a beautiful seagull in the air between them. The angles of elevation from the girls to the bird are 20° and 45°, respectively. How high up is the seagull? Round to three decimal places. Show your work.

Answer 1

`\huge\boxed{\sf h = 26.684\ feet}`

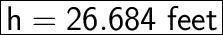
Explanation:

See the attached file along with the solution.

Let the height be h,

base of triangle 1 be x

base of triangle 2 be 100 - x

Using the following trigonometry for both the triangles.

`\displaystyle tan (\theta) = (opposite)/(adjacent)`

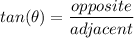
For triangle 1:

tan 20 = h / x ---------------------(1)

For triangle 2:

tan 45 = h / 100 - x -----------------(2)

Taking Eq. (1)

tan 20 = h / x

Multiply both sides by x

tan 20 * x = h

h = tan (20) * x

h = 0.36397x -----------------------(3)

Put Eq. (3) in (2)

tan (45) = 0.36397x / 100-x

1 = 0.36397 x / 100 - x

Multiply both sides by 100 - x

100 - x = 0.36397 x

Add x to both sides

100 = 0.36397 x + x

100 = 1.36397 x

Divide both sides by 1.36397

100 / 1.36397 = x

73.315 = x

x = 73.315 feet

Now, Finding h (height):

tan 20 = h / x (Eq. (1))

h = tan (20) * x

h = 0.36397 * 73.315

h = 26.684 feet

`\rule[225]{225}{2}`

Hope this helped!

~AH1807