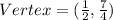Answer:
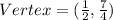
Explanation:
Given
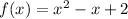
Required
The vertex
We have:
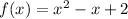
First, we express the equation as:
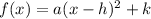
Where
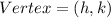
So, we have:
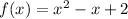
--------------------------------------------
Take the coefficient of x: -1
Divide by 2: (-1/2)
Square: (-1/2)^2
Add and subtract this to the equation
--------------------------------------------
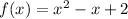
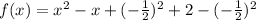
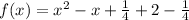
Expand
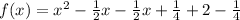
Factorize
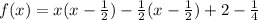
Factor out x - 1/2
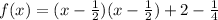
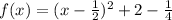

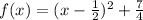
Compare to:
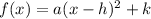
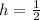
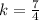
Hence: