Question

Please answer the question in the picture and show your work! I got tan= square root of 2 but I’m not sure if that’s right and if there’s more answers since it wants all values of tan. This is due tomorrow please help!

Answer 1

tan(θ) is undefined.

Explanation:

Recall that tan(θ) = sin(θ) / cos(θ). We are given that sin(θ) = -1. Hence:

`\displaystyle \tan\theta=(\sin\theta)/(\cos\theta)=-(1)/(\cos\theta)`

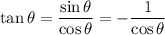
Since 1 / cos(θ) = sec(θ):

`\tan\theta=-\sec\theta`

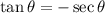
We can square both sides:

`\tan^2\theta=\sec^2\theta`

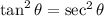
From the Pythagorean Identity:

`\tan^2\theta+1=\sec^2\theta`

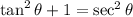
Substitute:

`\tan^2\theta+1=\tan^2\theta`

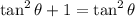
So:

`1\\eq0`

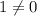
Since we acquire an untrue statement, no solutions exist.

If needed, refer to the unit circle. Recall that sin(θ) only equals -1 when θ = 3π/2 (on the interval [0, 2π)). At 3π/2, cos(θ) = 0. Since tan(θ) = sin(θ) / cos(θ), tan(θ) is undefined whenever sin(θ) = -1 (or 1).