Question

A banner is hung for a party. The distance from a point on the bottom edge of the banner to the floor can be determined by using the function f(x) = 0.25 x2 − x + 9.5 , where x is the distance, in feet, of the point from the left end of the banner. How high above the floor is the lowest point on the bottom edge of the banner? Explain.

Answer 1

That's possible when function tends to zero

`\\ \rm\hookrightarrow 0.25x^2-x+9.5=0`

`\\ \rm\hookrightarrow 1/4x^2-x+19/2=0`

`\\ \rm\hookrightarrow x^2-x+38=0`

`\\ \rm\hookrightarrow x=(1\pm√(1-152))/(2)`

`\\ \rm\hookrightarrow x=(1\pm√(151)i)/(2)`

Answer 2

8.5 ft

Explanation:

`f(x) = 0.25x^2 - x + 9.5`

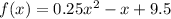
To find the minimum point of the function, differentiate:

`f'(x) = 0.5x - 1`

set to zero and solve for x:

`f'(x) =0\\ \implies0.5x - 1=0\\\implies x=2`

Substitute found value of x into function to find y (height):

`f(2) = 0.25(2)^2 - 2 + 9.5=8.5`

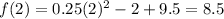
Therefore, the lowest point on the bottom edge of the banner is 8.5 ft above the floor.