Question

The curriculum director in a large 3 points school district wants to determine the difference between the proportion of high school juniors who are enrolled in AP classes and the proportion of high school seniors who are enrolled in AP classes. She randomly selects 75 seniors and 70 juniors. Twenty-six of the seniors are enrolled in AP classes and 15 of the juniors are enrolled in AP classes. A 90 percent confidence interval for the difference between the proportion of seniors and juniors who are enrolled in AP classes is calculated. Which statement is not true?

A) The critical value used is 1.645.
B) The standard error of the difference is 0.074
C) The 90% interval was constructed using a method that results in intervals which capture the true difference in the proportion of seniors who are enrolled in AP classes and the proportion of juniors who are enrolled in AP classes 90% of the time.
D) She can be 90% confident that the true difference between the proportion of seniors who are enrolled in AP classes and the proportion of juniors who are enrolled in AP classes is between 0.0112 and 0.2535 students.
E) There is a 90% chance that the true difference between the proportion of seniors who are enrolled in AP classes and the proportion of juniors who are enrolled in AP classes is between 0.0112 and 0.2535

Answer 1

C) The 90% interval was constructed using a method that results in intervals which capture the true difference in the proportion of seniors who are enrolled in AP classes and the proportion of juniors who are enrolled in AP classes 90% of the time.

Explanation:

x% confidence interval -> Options c, d and e:

A confidence interval is built from a sample, has bounds a and b, and has a confidence level of x%. It means that we are x% confident that the population mean is between a and b.

This means that options d and e are correct, while option c is not true.

Option a -> Critical Value:

90% confidence level

So
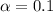`\alpha = 0.1`, z is the value of Z that has a p-value of
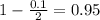`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

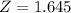This means that option A is true.

Estimate of the standard error:

Before building the estimate, we should take a look at the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

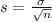For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
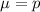`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

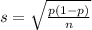
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

26 of 75 seniors:

This means that:

`p_s = (26)/(75) = 0.3467, s_s = \sqrt{(0.3467*0.6533)/(75)} = 0.055`

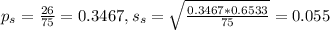
15 of 70 juniors:

This means that:

`p_j = (15)/(70) = 0.2143, s_j = \sqrt{(0.2143*0.7857)/(70)} = 0.049`

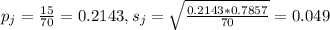
Estimate of the standard error:

`s = √(s_s^2 + s_j^2) = √(0.055^2 + 0.049^2) = 0.074`

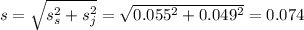
Thus option b is correct.