Question

Billy has a gallon of paint. He us going to pour it into a paint tray that measures 10 inches wide, 14 inches long and 4cm deep. What will happen

Answer 1

Tray will overflow with
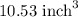`10.53\ \text{inch}^3` of paint.

Explanation:

Dimensions the tray is 10 inch by 14 inch by 4 cm

`1\ \text{cm}=(1)/(2.54)\ \text{inch}`

`4\ \text{cm}=(4)/(2.54)\ \text{inch}`

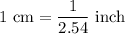
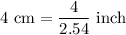
Volume the tray can hold is

`10* 14* (4)/(2.54)\ \text{in}^3`

`1\ \text{inch}^3=(1)/(231)\ \text{gallon}`

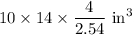
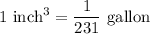
The volume of paint Billy has is
`1\ \text{gallon}`

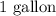
Difference in the volume of paint and volume of tray in cubic inches is

`\left(1-(10*14*(4)/(2.54))/(231)\right)231=10.53\ \text{inch}^3`

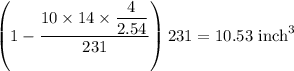
The tray will overflow with
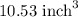`10.53\ \text{inch}^3` of paint.