Question

A, B & C lie on a straight line.

D, C & E lie on a different straight line.
Angle
y
= 96° and angle
z
= 52°.
Work out
x

Answer 1

x = 136°

Explanation:

∠ABD = y = 96°, ∠ABD + ∠DBC must be equal to 180° because they form a straight angle.

`y + B = 180\\96 + B = 180\\B = 180 - 96 = 84`

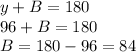
∠BDC = z = 52° and ∠DBC = B = 84.

Angles ∠BDC, ∠DBC, and ∠BCD must have a sum of 180° because the sum of the interior angles in a triangle is 180°.

`180=(180 - y) + 52 + C\\180=(180 - 96) + 52 + C\\180 - (52 + 84) = C\\C = 44`

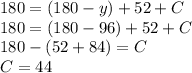
The interior angle at C is 44. Line DCE forms a straight line, therefore having an angle of 180°. To find x, the sum of x and interior angle C is 180°.

`180 = C + x\\180 = 44 + x\\x = 180-44\\x = 136\\`

Angle ∠BCE = x = 136.

Answer 2

x = 136°

Explanation:

We can use a theorem to help us.

Theorem:

The measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles.

For exterior angle x, the remote interior angles are z and <CBD.

From the theorem, we get this equation.

x = z + m<CBD

We know z = 52°.

We need to find m<CBD.

Angles CBD and y are a linear pair. They are supplementary, so the sum of their measures is 180°. We are given y = 96°.

m<CBD + y = 180°

m<CBD + 96° = 180°

m<CBD = 84°

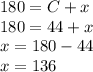
x = z + m<CBD

x = 52° + 84°

x = 136°