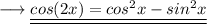Question

Futhe Mathematics

`(Cos {}^(4)t -Sin {}^(4)t ) / Cos {}^(2)t`
​

Answer 1

cos2t/cos²t

Explanation:

Here the given trigonometric expression to us is ,

`\longrightarrow (cos^4t - sin^4t )/(cos^2t )`

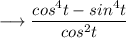
We can write the numerator as ,

`\longrightarrow ( (cos^2t)^2-(sin^2t)^2)/(cos^2t )`

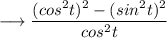
Recall the identity ,

`\longrightarrow (a-b)(a+b)=a^2-b^2`

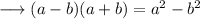
Using this we have ,

`\longrightarrow ((cos^2t + sin^2t)(cos^2t-sin^2t))/(cos^2t)`

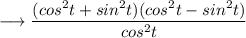
Again , as we know that ,

`\longrightarrow sin^2\phi + cos^2\phi = 1`

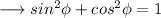
Therefore we can rewrite it as ,

`\longrightarrow (1(cos^2t - sin^2t))/(cos^2t)`

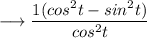
Again using the first identity mentioned above ,

`\longrightarrow \underline{\underline{((cost + sint )(cost - sint))/(cos^2t)}}`

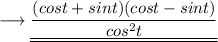
Or else we can also write it using ,

`\longrightarrow cos2\phi = cos^2\phi - sin^2\phi`

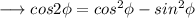
Therefore ,

`\longrightarrow \underline{\underline{(cos2t)/(cos^2t)}}`

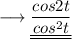
And we are done !

`\rule{200}{4}`

Additional info :-

Derivation of cos²x - sin²x = cos2x :-

We can rewrite cos 2x as ,

`\longrightarrow cos(x + x )`

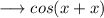
As we know that ,

`\longrightarrow cos(y + z )= cosy.cosz - siny.sinz`

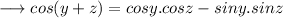
So that ,

`\longrightarrow cos(x+x) = cos(x).cos(x) - sin(x)sin(x)`

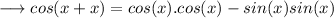
On simplifying,

`\longrightarrow cos(x+x) = cos^2x - sin^2x`

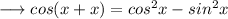
Hence,

`\longrightarrow\underline{\underline{cos (2x) = cos^2x - sin^2x }}`

`\rule{200}{4}`