Answer:
(D) Expression I and expression Il evaluate to the same value only when A and B differ.
Step-by-step explanation:
Given
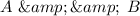
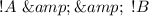
Required
Select the true statement
To do this, I will create the following case scenarios.
(a):
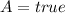 and
and
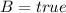
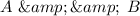
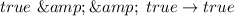 i.e. true and true is true
i.e. true and true is true
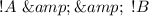
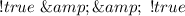
------------------------------------------------------
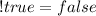
------------------------------------------------------
So, we have:
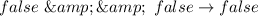
So:
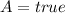 and
and
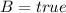
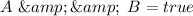
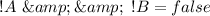
Hence, options (B) and (E) are incorrect
(b):
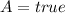 and
and
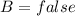
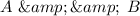
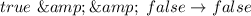
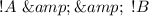
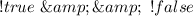
Solve each negation
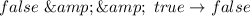
So:
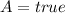 and
and
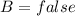
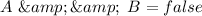
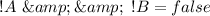
Hence, option (c) is incorrect
(c):
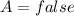 and
and
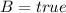
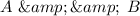
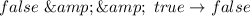
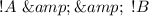
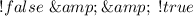
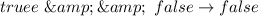
So:
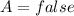 and
and
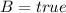
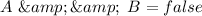
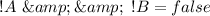
Case scenarios b and c implies that option (d) is correct because different values of A and B gives the same value of both expression which is false
This also implies that (a) is incorrect.