Question

Consider the following data that represents gas mileages per gallon (mpg) of randomly selected cars of a particular brand.

28 32 23 28 24 36 31 34 25 28 29 23 25

A researcher wants to test whether the average gas mileage of this type of car is different from 30 mpg. Compute the p-value.

Answer 1

The p-value is 0.1228.

Explanation:

Before testing the hypothesis, we need to find the sample mean and the standard deviation.

Sample of 13:

The sample mean is the sum of all values divided by 13. Using a calculator, it is: X = 28.15.

The sample standard deviation is the square root of the division of the sum of the differences squared between each value and the mean, by the number of values. Using a calculator, we get s = 4.0162.

A researcher wants to test whether the average gas mileage of this type of car is different from 30 mpg.

At the null hypothesis, we test if the average gas mileage is of 30 mpg, that is:

`H_0: \mu = 30`

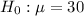
At the alternate hypothesis, we test if the average is different from 30, that is:

`H_1: \mu \\eq 30`

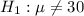
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

30 is tested at the null hypothesis:

This means that
`\mu = 30`

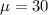
From the sample:

`X = 28.15, s = 4.0162`.

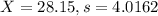Value of the test-statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (28.15 - 30)/((4.0162)/(√(13)))`

`t = -1.66`

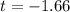
P-value of the test:

The p-value of the test is the probability that the sample mean differs from 30 by at least |28.15 - 30| = 1.75, which is a two-tailed test with t = -1.66 and 13 - 1 = 12 df.

Using a t-distribution calculator, this p-value is 0.1228.