Answer:
No, this triangle is not a right triangle.
Explanation:
Step 1: Definition(s)/explanations
- This is a right triangle, so the Pythagorean Theorem applies.
- The Pythagorean Theorem states that the legs of the triangle, squared, must equal the hypotenuse, squared.
- The legs of the triangle are the sides that make the right angle.
- The hypotenuse is the longest side.
Formula:
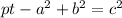
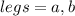
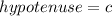
Step 2: Solve.
Now, I just plug the numbers into the formula.

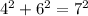
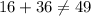
If the legs of the triangle do not equal the hypotenuse, then the triangle cannot be a right triangle.
Step 3: Conclude.
Therefore, the triangle cannot be a right triangle.