Question

Mr. Pratt was building a house. A ladder that is 10 ft. long is leaning against the side of a building. If the angle formed between the ladder and the ground is 65 degrees, how far is the bottom of the ladder from the base of the building? Round to one decimal place.

Answer 1

4.2 feet

Explanation:

.................

Answer 2

`\huge\boxed{\text{4.2 feet}}`

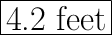
Explanation:

In order to solve this problem, we can use the basic trigonometric functions.

Let's first start to break down the triangle scenario we're given.

• We know that the ladder is 10 ft tall. Given that it is slanted, it's likely the hypotenuse.

• We know the angle formed between the ladder and the ground is 65°. Since the ladder will form a 90° angle with the ground, the last angle will have to follow the triangle rule.
• The triangle rule is that all angles within a triangle will add up to 180°. Using this logic, we can find the measure of the third angle from the other two

• 
  `90+65+x=180`,
  `155+x=180`,
  `x=25`

Now we know the three angles of the triangle and one side.

We can find the other two sides (or just the base side, in our case), using trigonometric functions such as sin, cos, and tan. We can substitute in their formulas and find lengths based on angle measures.

We know using SOH CAH TOA the relationships between opposites, adjacents, and hypotenuses with these functions. SOH CAH TOA states that:

1. Sin = Opposite/Hypotenuse
2. Cosine = Adjacent/Hypotenuse
3. Tangent = Opposite/Adjacent

Using the triangle, we want to find a relationship that has the base we need as an opposite/adjacent that can use the hypotenuse (since it's the only side length we know.

Well, we can take the sin of the 25 degree angle - it's opposite is the base leg and the hypotenuse is 10.

We can then represent this using an equation:

• 
  `\text{sin}(25) = \frac{\text{opposite}}{\text{hypotenuse}}`
• 
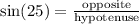
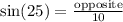  `\text{sin}(25) = \frac{\text{opposite}}{10}` (Since we know the hypotenuse is 10)
• 
  `\text{sin}(25) \cdot 10 = \text{opposite}`
• We know that sin(25) is roughly 0.4226 because of our. calculator. We can then multiply that by 10 to recieve 4.226. This rounds to 4.2 (to the nearest 10th).

Therefore, the length of the base leg is 4.2 feet

Hope this helped!