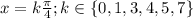Answer:
If
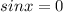 we get
we get
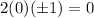 which is true. so we have a first set of solutions given by
which is true. so we have a first set of solutions given by
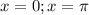 ;
;
Else, if
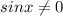 we can divide both sides by it and we get
we can divide both sides by it and we get
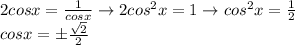
Which gives us a second set of solutions given by
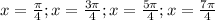 ;
;
We can group all solutions (doesn't matter, but it's more elegant!) by writing