Answer:
See below directions.
Explanation:
The condition
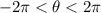 means you can get to the point by rotating no more than one revolution in either the positive or negative direction.
means you can get to the point by rotating no more than one revolution in either the positive or negative direction.
See the attached image to see the point
 . Think about how you get to that point: start at the origin, go right (along the positive x-axis) 3 units, then turn in the negative direction (to your right!) through an angle of
. Think about how you get to that point: start at the origin, go right (along the positive x-axis) 3 units, then turn in the negative direction (to your right!) through an angle of
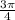 .
.
Now, go again, starting at the origin, only this time, go 3 units right, then turn through an angle of
 . In other words, you turn one whole revolution in addition to the
. In other words, you turn one whole revolution in addition to the
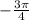 angle. Your point can now be described by
angle. Your point can now be described by
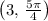 .
.
Another description can be found by rotating in the opposite direction, so an angle of
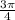 and backing up 3 units -- specify a "radius" of -3. The point is then
and backing up 3 units -- specify a "radius" of -3. The point is then
 .
.
You can also try subtracting one revolution
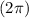 from the angle, but be careful not to let the angle go outside the interval
from the angle, but be careful not to let the angle go outside the interval
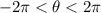 .
.
The changes you can try are:
add
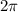 to the angle, leave r alone
to the angle, leave r alone
subtract
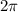 to the angle, leave r alone
to the angle, leave r alone
add/subtract
 (half a revolution) to the angle, make r the opposite.
(half a revolution) to the angle, make r the opposite.