Question

Water in an electric teakettle is boiling. The power absorbed by the water is 0.90 kW. Assuming that the pressure of vapor in the

kettle equals atmospheric pressure, determine the speed of effusion of vapor from the kettle's spout if the spout has a cross-
sectional area of 1.60 cm2. Model the steam as an ideal gas.​

Answer 1

v = 4.233 m/s

Step-by-step explanation:

By applying the rate of boiling from
`Q= mL_v`;

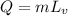the rate of the boiling can be described as:

`\mathcal{P} = (Q)/(\Delta t) \\ \\ \mathcal{P} = (mL_v)/(\Delta t)`

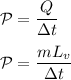
The mode of the steam (water vapor) as an ideal gas can be illustrated by formula:

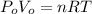`P_oV_o = nRT` --- (1)

where;

n = number of moles;

`n = (mass (m))/(Molar mass (M))`

Then; equation (1) can be rewritten as:

`P_oV_o = ((m)/(M)) RT \\ \\ (P_oV)/(\Delta T) = (m)/(\Delta t) ( (RT)/(M))`

∴

`(m)/(\Delta t) = \frac{\mathcal{P}}{L_v}`

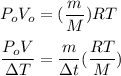
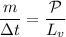
Then:

`P_o * A * v= \frac{\mathcal{P}}{L_v}\Big ( (RT)/(M )\Big)`

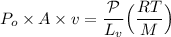
making (v) the subject of the formula:

`v= \Big ( \frac{\mathcal{P} RT}{M* L_v * P_o * A }\Big)`

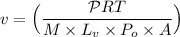
Given that:

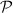`\mathcal{P}` = 0.90 kW = 900 W

R(rate constant) = 8.314 J/mol.K

Temperature at 100° C = 373K

For water vapor:

molar mass= 18.015 g/mol ≅ 0.0180 kg/mol

Latent heat of vaporisation
`L_v` = 2.26 × 10⁶ J/kg

Atmospheric pressure
`P_o = 1.013 * 10^6 \ N/m^2`

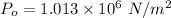
Cross sectional area A =1.60 cm² = 1.60 × 10⁻⁴ m²

`v= \Big ( (900 W (8.314 \ J/mol.K)(373))/(0.0180 \ kg/mol) (2.26 * 10^6 \ J/kg) (1.013 * 10^5 \ N/m^2)(1.60 * 10^(-4) \ m^2))\Big)`

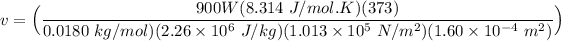
v = 4.233 m/s