Question

Bern is flying a kite directly over his friend Frank. Bern lets out string which makes an angle of 28°

with the ground. If the kite is 175 feet above Frank, how far are Bern and Frank?
Help ASAP!!

Answer 1

orayt so 28 degree and 175 feet is about...the fox jumps into the lazy dog and say "c'mon barbie let's go party! ah ah ah yeah"....but i dont know the answer as well so thank you.

Answer 2

Approximately
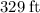`329\; \rm ft`, assuming that the ground between Bern and Frank is level.

Explanation:

Refer to the diagram attached.

The kite is right above Frank. Therefore, the imaginary line segment (the dashed line segment in the diagram) would form a right angle with the ground under Frank. Bern, Frank, and the Kite would be the three vertices of a right triangle.

The question states that from the perspective of Bern, the angle of elevation of the kite is
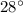`28^\circ`. In this right triangle, the side opposite to this angle would be the imaginary line segment between Frank and the kite over him. The question states that the length of this imaginary line segment is
`175\; \rm ft`.

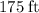The question is asking for the length of the line segment between Bern and Frank. In the right triangle pictured in this diagram, that line segment would be the side adjacent to the
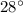`28^\circ` angle.

The cotangent of
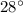`28^\circ` would be the ratio between the length of these two sides:

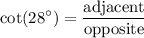`\displaystyle \cot (28^\circ) = \frac{\text{adjacent}}{\text{opposite}}`.

`\begin{aligned}\text{adjacent} &= \text{opposite} \cdot \cot(28^\circ) \\ &= (175\; \rm ft) \cdot \cot(28^\circ) \approx 329\; \rm ft\end{aligned}`.