Question

Find the distance between the two points rounding to the nearest tenth (if necessary).

(-1,5) and (4, -7)

Answer 1

13

Explanation:

The difference between the x-values is 5.

The difference between the y-values is 12.

These are the non-hypotenuse sides.

12^2 + 5^2 = c^2

144 + 25 = c^2

169 = c^2

c = 13

The distance between the two points is 13.

Answer 2

13 units

Explanation:

(-1,5) and (4, -7)

To find the distance of two points, we use the distance formula:

`d = \sqrt{(x_(2)-x_1)^2 + (y_2-y_1)^2 }`

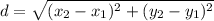
Let's plug in what we know.

`d = √((4 - (-1))^2 + (-7 - 5)^2 )`

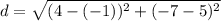
Evaluate the double negative.

`d = √((4 +1))^2 + (-7 - 5)^2 )`

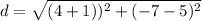
Evaluate the parentheses.

`d = √((5)^2 + (-12)^2 )`

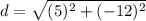
Evaluate the exponents.

`d = √((25) + (144) )`

Add.

`d = √((169) )`

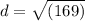
Evaluate the square root.

`d = 13`

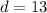
13 units

Hope this helps!