Question

a deep underground cavern contains 2.24 x 10^6 L of methane (CH4) gas at a pressure of 15.0 atm and a temperature of 42 C. How many moles of methane does this natural gas deposit contain?

Answer 1

This natural gas deposit contains 1,300,813.008 moles.

Step-by-step explanation:

An ideal gas is a theoretical gas that is considered to be composed of point particles that move randomly and do not interact with each other. Gases in general are ideal when they are at high temperatures and low pressures.

An ideal gas is characterized by three state variables: absolute pressure (P), volume (V), and absolute temperature (T). The relationship between them constitutes the ideal gas law, an equation that relates the three variables if the amount of substance, number of moles n, remains constant and where R is the molar constant of the gases:

P * V = n * R * T

In this case:

• P= 15 atm
• V=2.24*10⁶ L
• n= ?
• R= 0.082
  `(atm*L)/(mol*K)`
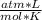
• T= 42 C= 315 K (being 0 C= 273 K)

Replacing:

15 atm* 2.24*10⁶ L= n*0.082
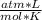`(atm*L)/(mol*K)`* 315 K

Solving:

`n=(15 atm* 2.24*10^(6)L )/(0.082(atm*L)/(mol*K)*315 K)`

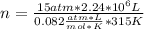
n=1,300,813.008 moles

This natural gas deposit contains 1,300,813.008 moles.