Question

For positive acute angles AA and B,B, it is known that \sin A=\frac{8}{17}sinA= 17 8 ​ and \cos B=\frac{24}{25}. CosB= 25 24 ​. Find the value of \sin(A+B)sin(A+B) in simplest form

Answer 1

sin(A+B) = 297/425

Explanation:

This problem involves a couple of Pythagorean triples, and the trig identity for the sine of the sum of angles.

The Pythagorean triples involved are {8, 15, 17} and {7, 24, 25}. These tell us the other trig functions of the given angles:

sin(A) = 8/17 ⇔ cos(A) = 15/17

cos(B) = 24/25 ⇔ sin(B) = 7/25

The trig identity we're using is ...

sin(A+B) = sin(A)cos(B) +cos(A)sin(B)

sin(A+B) = (8/17)(24/25) +(15/17)(7/25)

`\sin(A+B)=(8\cdot24+15\cdot 7)/(17\cdot25)\\\\\boxed{\sin(A+B)=(297)/(425)}`

_____

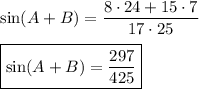
Check

A = arcsin(8/17) ≈ 28.072°

B = arccos(24/25) ≈ 16.260°

sin(A+B) = sin(44.332°) ≈ 0.6988235

sin(A+B) = 297/425