Question

A group of 25 people are going to run a race. The top 8 finishers advance to the finals. Determine the number of possible outcomes.

Answer 1

`\large\boxed{ \boxed{\rm 1081575 \: outcomes}}`

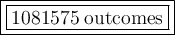
Explanation:

to determine the number of possible outcomes we can consider Combination given by

`\displaystyle \binom{n}{r} = (n!)/(r!(n - r)!)`

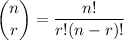
where:

• n is the total number of objects in the set
• r is the number of choosing objects from the set

so let n and r be 25 and 8 respectively thus

substitute:

`\displaystyle \binom{25}{8} = (25!)/(8!(25- 8)!)`

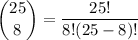
simplify parentheses:

`\displaystyle \binom{25}{8} = (25!)/(8! * 17!)`

rewrite numeratorr:

`\rm \displaystyle \binom{25}{8} = (25 * 24 * 23 * 22 * 21 * 20 * 19 * 18 * 17!)/(8! * 17!)`

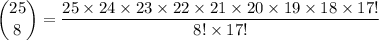
reduce fraction:

`\rm \displaystyle \binom{25}{8} = (25 * 24 * 23 * 22 * 21 * 20 * 19 * 18 )/(8! )`

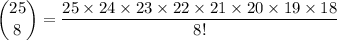
simplify numerator and denominator:

`\rm \displaystyle \binom{25}{8} = (43609104000)/(40320 )`

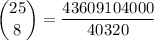
simplify division:

`\rm \displaystyle \binom{25}{8} = 1081575`

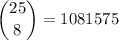
hence,

the number of outcomes is 1081575

Answer 2

n[total]=25

n[top finishers]=8

the number of possible outcome

=
`(25 * 24 * 23 * 22 * 21 * 20 * 19 * 18)/(8 * 7 * 6 * 5 * 4 * 3 * 2 * 1) = 1081575`outcomes