The option are missing in the question. The options are :
A. P = 2, a = 1
B.
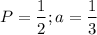
C.
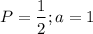
D. P = 2, a = 3
Solution :
The given function is
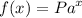
So for the function to be an exponential growth, a should be a positive number and should be larger than 1. If it less than 1 or a fraction, then it is a decay. If the value of a is negative, then it would be between positive and negative alternately.
When the four option being substituted in the function, we get
A). It is a constant function since
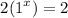
B). Here, the value of a is a fraction which is less than 1, so it is a decay function.
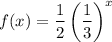
C). It is a constant function since the value of a is 1.
D). Here a = 3. So substituting, as the value of x increases by 1, the value of the function, f(x) increases by 3 times.
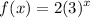
Therefore, option (D). represents an exponential function.