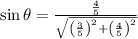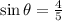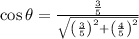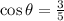Question

If the terminal side of angle 0 in standard position intersects the unit circle at p (3/5,4/5). Find cos0 and sin0

Answer 1

`\sin \theta = (4)/(5)`,
`\cos \theta = (3)/(5)`

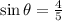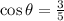
Explanation:

Let be
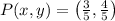`P(x,y) = \left((3)/(5), (4)/(5) \right)` the end of the terminal side of angle
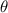`\theta` in standard position, that is, an angle measured with respect to +x semiaxis. By Trigonometry, we know that the sine and the cosine of the angle are, respectively:

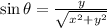`\sin \theta = \frac{y}{\sqrt{x^(2) + y^(2)}}` (1)

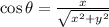`\cos \theta = \frac{x}{\sqrt{x^(2)+y^(2)}}` (2)

If we know that
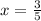`x = (3)/(5)` and
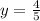`y = (4)/(5)`, then the sine and the cosine of the angle are:

`\sin \theta = \frac{(4)/(5) }{\sqrt{\left((3)/(5) \right)^(2)+\left((4)/(5) \right)^(2)}}`

`\sin \theta = (4)/(5)`

`\cos \theta = \frac{(3)/(5) }{\sqrt{\left((3)/(5) \right)^(2)+\left((4)/(5) \right)^(2)}}`

`\cos \theta = (3)/(5)`