Question

6. A stoplight at an intersection stays red for 60 second, changes to green for 45

seconds, and then turns yellow for 15 seconds. If Jamal arrives at the

intersection at a random time, what is the probability that he will have to wait at

a red light for more than 15 seconds?

Answer 1

0.75 = 75% probability that he will have to wait at a red light for more than 15 seconds

Explanation:

At each second, the stoplight is equally likely to change, which means that we use the uniform probability distribution to solve this question.

Uniform probability distribution:

Has two bounds, a and b. The probability of finding a value higher than x is given by:

`P(X > x) = (b - x)/(b - a)`

Red for 60 seconds

So when Jamal arrives it can change in any number of seconds between 0 and 60, that is,
`a = 0, b = 60`

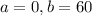
Probability that he will have to wait at a red light for more than 15 seconds?

`P(X > 15) = (60 - 15)/(60 - 0) = (45)/(60) = (3)/(4) = 0.75`

0.75 = 75% probability that he will have to wait at a red light for more than 15 seconds