Question

Find the derivative of


`y = (3)/(2x ^(2) )`
at the point

`(1. (3)/(2) )`

​

Answer 1

`\displaystyle y'(1, (3)/(2)) = -3`

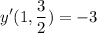
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Coordinates (x, y)
• Functions
• Function Notation
• Terms/Coefficients
• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

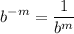
Calculus

Derivatives

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

`\displaystyle y = (3)/(2x^2)`

`\displaystyle \text{Point} \ (1, (3)/(2))`

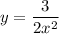
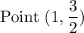
Step 2: Differentiate

1. [Function] Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y = (3)/(2)x^(-2)`
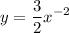
2. Basic Power Rule:
   `\displaystyle y' = -2 \cdot (3)/(2)x^(-2 - 1)`
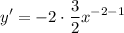
3. Simplify:
   `\displaystyle y' = -3x^(-3)`
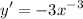
4. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y' = (-3)/(x^3)`

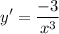
Step 3: Solve

1. Substitute in coordinate [Derivative]:
   `\displaystyle y'(1, (3)/(2)) = (-3)/(1^3)`
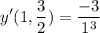
2. Evaluate exponents:
   `\displaystyle y'(1, (3)/(2)) = (-3)/(1)`
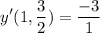
3. Divide:
   `\displaystyle y'(1, (3)/(2)) = -3`

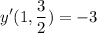
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e