Answer:
a. v = 340.27 m/s
b. t = 0.15 s
Step-by-step explanation:
a.
The speed of sound at any given temperature can be found out by the use of the following formula:
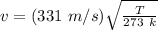
where,
T = Absolute temperature = 15.5°C + 273 = 288.5 k
therefore,
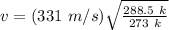
v = 340.27 m/s
b.
The time of echo to return can be found by the following formula:
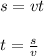
where,
t = time = ?
s = distance = (2)(25 m) = 50 m
v = speed of sound = 340.27 m/s
Therefore,
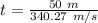
t = 0.15 s