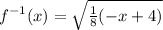Question

Identify the inverse of the following.

Answer 1

`f^(-1)(x)=\sqrt{(1)/(8)(-x+4)}`

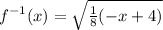
Explanation:

Given function is,

f(x) = -8x² + 4

Step to find the inverse of the function,

Step 1

Write the function in the form of an equation,

y = -8x² + 4

Step 2

Interchange the variables 'x' and 'y',

x = -8y² + 4

Step 3

Solve the equation for y,

x = -8y² + 4

x - 4 = -8y²

-x + 4 = 8y²

y² =
`(1)/(8)(-x+4)`

`y=\sqrt{(1)/(8)(-x+4)}`

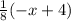
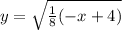
Therefore, inverse of the function f(x) will be,

`f^(-1)(x)=\sqrt{(1)/(8)(-x+4)}`