Question

Robert spun the fair spinner shown below 1,060 times,

About how many times would Robert expect to spin a 1, 3, or 8?

Answer 1

About 400 times

Explanation:

Given

`n = 1060`

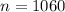
See attachment for spinner

Required

Determine the number of times an outcome of 1, 3 or 8 is expected

First, calculate the theoretical probability of 1, 3, or 8

This is calculated as:

`Pr = P(1) + P(3) + P(8)`

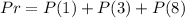
The spinner is divided into 8 equal segments and each outcome appears once.

So, we have:

`Pr = (1)/(8)+(1)/(8)+(1)/(8)`

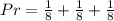
Take LCM and add

`Pr = (1+1+1)/(8)`

`Pr = (3)/(8)`

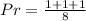
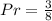
So, the expected number of times (E) is:

`E = Pr * n`

`E = (3)/(8) * 1060`

`E = (3* 1060)/(8)`

`E = (3180)/(8)`

`E = 397.5`

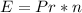
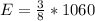
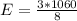
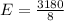
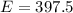
Approximate

`E = 398`

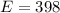
This means about 400 times