Answer:
The times that would take until the cylinder is completely full with water by the cone are:
Explanation:
To identify how many times we must fill a cone to fill completely a cylinder with the same height and radius, we must calculate the volume of the two containers and next divide the volume of the cylinder by the volume of the cone. To obtain the volume of the cylinder we can use the next formula:
- Volume of a cylinder =
 *
*
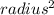 *
*
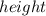
If we replace the values in the formula, we obtain:
- Volume of a cylinder =
 *(5 inches)^2 * 10 inches
*(5 inches)^2 * 10 inches - Volume of a cylinder = 785.4 inches^3 approximately.
Now, we're gonna calculate the volume of the cone with the next formula:
- Volume of a cone =
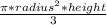
As you can see just with the formula, The volume of a cone is three times less than that of a cylinder (because we add the dividend 3 to it), but we're gonna replace and prove it:
- Volume of a cone = [
 *(5 inches)^2 * 10 inches] / 3
*(5 inches)^2 * 10 inches] / 3 - Volume of a cone = [785.4 inches^3] / 3
- Volume of a cone = 261.8 inches^3 approximately.
And, if we divide the two volumes to obtain the times we need to fill the cone to fill completely the cylinder:
- Times we need to fill the cone = 785.4 / 261.8
- Times we need to fill the cone = 3
By this reason, you must fill completely a cone 3 times to fill completely a cylinder with the same radius and height.