Question

A conservationist is tracking the number of a rare type of tree in a forest as it recovers from a fire.

During the first 4 years after the fire, she records 2, 6, 18, and 54 trees. If this trend continues, which

expression can be used to find the number of trees after n years?

Answer 1

The expression is
`T(n) = 2*(3)^n`

Explanation:

Geometric sequence:

In a geometric sequence, the quotient between consecutive terms is always the same.

The general rule of an geometric sequence is given by:

`T(n) = T(0)(q)^n`

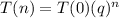
In which T(0) is the initial amount and q is the quotient.

During the first 4 years after the fire, she records 2, 6, 18, and 54 trees.

First term is 2, so
`T(0) = 2`.

Quotient is
`q = (54)/(18) = (18)/(6) = (6)/(2) = 3`

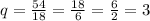
So

`T(n) = T(0)(q)^n`

`T(n) = 2*(3)^n`

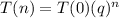
The expression is
`T(n) = 2*(3)^n`