Answer:
a) The volume of the box is represented by
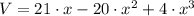 .
.
b) A side length of 0.653 inches leads to the maximum volume of the box: 6.299 inches.
Explanation:
a) The volume of the box (
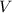 ), in cubic inches, is modelled by the equation for the cuboid:
), in cubic inches, is modelled by the equation for the cuboid:
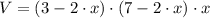 (1)
(1)
Where
 is the side length of the cutted square corners, in inches.
is the side length of the cutted square corners, in inches.
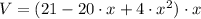
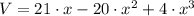
The volume of the box is represented by
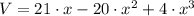 .
.
b) The method consist in graphing the polynomial and looking for a relative maximum. We graph the equation found in a) by means of a graphic tool. We present the outcome in the image attached below. According to this, a side length of 0.653 inches leads to the maximum volume of the box: 6.299 inches.